La eterna pregunta: ¿Cuándo una diferencia entre medias es estadísticamente significativa? En cualquier análisis
estadístico la información más habitual que se presenta en los informes es
la Media Aritmética. Es un resultado
sencillo y de fácil compresión, sin embargo, en multitud de foros y reuniones
de trabajo surge la pregunta a la hora de comparar 2 medias.
Si estamos afirmando que A (sea una tienda, paciente, proveedor)
vende un promedio de 140 unidades al mes este año y el año anterior vendía 149
… ¿Esta diferencia es estadísticamente
significativa?
El resolver esta pregunta implica realizar un test de hipótesis ya que es la herramienta matemática que cuantifican hasta
qué punto la variabilidad de la muestra puede ser responsable de los resultados
de un estudio en particular. La Ho (hipótesis nula) representa la
afirmación de que no hay asociación entre las dos variables estudiadas y la Ha
(hipótesis alternativa) afirma que hay algún grado de relación o asociación.
Nuevamente la estadística nos muestra su utilidad ya que nos ayuda a tomar
la decisión de que hipótesis debemos elegir. Dicha decisión puede ser afirmada
con una seguridad que nosotros previamente decidimos y que denominamos Nivel de
Significación.
¿Cómo se realiza un test de hipótesis?
Aunque con matices, se realizan de la siguiente forma. En primer lugar se
mira la magnitud de la diferencia que hay entre los grupos a comparar (A y B).
Si esta magnitud o valor absoluto es mayor que un error estándar definido
multiplicado por una seguridad definida, concluimos que la diferencia es
significativa entre A y B. Por tanto aceptamos la hipótesis alternativa y
rechazamos la hipótesis nula.
Ejemplo:
Disponemos de 2 tratamientos ( A y B). El tratamiento A lo reciben 25
pacientes y el tratamiento B otros 25 pacientes. 15 pacientes responden
favorablemente al tratamiento A y 20 al tratamiento B. ¿Existe diferencia
significativa entre ambos tratamientos?
Ho (hipótesis nula) = No hay diferencia entre ambos
tratamientos.
Ha (hipótesis alternativa) = Sí existe diferencia.
Error estándar * 1.96 = 0.1296 * 1.96 = 0.25
Como quiera que la diferencia = | 0,60 - 0,80 | = 0,20
|
no supera el
valor 0.25 concluimos que la diferencia entre 0.60 y 0.80 no es estadísticamente significativa. A la vista de los resultados no podemos
aceptar la Ha (hipótesis alternativa).
|
El proceso de aceptación o rechazo de la hipótesis lleva implícito un
riesgo que se cuantifica con el valor de la "p", que es la
probabilidad de aceptar la hipótesis alternativa como cierta, cuando la cierta
podría ser la hipótesis nula.



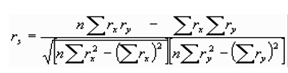



 ), entonces el 95% de las veces se
cumple:
), entonces el 95% de las veces se
cumple: