Hablamos de correlación cuando nos referimos a la relación existente entre dos variables, su intensidad y su sentido (positivo o negativo).
La covarianza definida anteriormente como promedio de desviaciones conjuntas de dos variables sobre sus respectivas medias, no resulta ser una medida adecuada de la relación entre dos variables, pues el valor de Sxy está relacionado con el valor de la media de X y con el valor de la media de Y. por este motivo, si cambiamos la unidad de medida, la covarianza se vera modificada.
Podemos afirmar que el valor de la covarianza depende de la unidad de medida. Para evitar el efecto de la unidad de medida sobre Sxy podemos dividir las puntuaciones diferenciales por las respectivas desviaciones típicas Sx y Sy. El nuevo índice de relación que obtengamos tendrá la ventaja de ser invariante ante cualquier cambio en la unidad de medida. A este índice de correlación se le denomina coeficiente de correlación de Pearson o también coeficiente de correlación producto momento.
Aplicar el coeficiente de correlación de Pearson exige que las variables estén medidas al menos en una escala de intervalos y que se de una relación lineal entre ellas. Es decir, que los puntos del diagrama de dispersión se posicionen en la forma aproximada de una línea recta. Por tanto, usar el coeficiente de correlación de Pearson presupone la sospecha de que entre los grupos de puntuaciones se da una relación lineal.
El valor del coeficiente de correlación de Pearson se encuentra comprendido entre -1 y 1.
• Valores próximos a 1 indicarán fuerte asociación lineal positiva.
• Valores próxi¬mos a -1 indicarán fuerte asociación lineal negativa.
• Valores próximos a 0 indicarán no asociación lineal, lo que no significa que no pueda existir otro tipo de asociación.
Resulta difícil precisar a partir de que valor de rxy podemos considerar que existe una correlación lineal entre dos variables. Siempre debemos tener en cuenta para la interpretación el tipo de variables a las que se aplica. Sin embargo, para tener un referente, y siendo conscientes de que estos coeficientes no son aplicables a todas las situaciones, tomamos los determinados por Bisquerra:
Además debemos tener presente que la existencia de una correlación no implica que necesariamente deba existir una relación causal directa. Por relación causal directa se entiende que si X e Y están correlacionadas, entonces X es en gran parte la causa de Y, o Y es en parte la causa de X.
No obstante, es habitual que tras encontrar una elevada correlación entre variables se hipoteticen relaciones causa efecto. Pero la existencia de una relación de este tipo habrá de ser comprobada recurriendo a otras estrategias de investigación y a otras técnicas estadísticas.

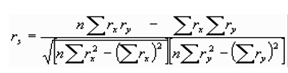

No hay comentarios:
Publicar un comentario